Zur Ableitung des Multiplikators folgen wir exakt der zitierten Vorgehensweise Keynes', notieren die einzelnen Schritte der Klarheit wegen in Gleichungen. Da sich das Einkommen aus Konsum und Investitionen zusammensetzt, kann eine Veränderung des Einkommens ΔY nur aus einer Veränderung des Konsums ΔC und einer Veränderung der Investitionen ΔI bestehen:
[1] ΔY = ΔC + ΔI.
Das Verhältnis der Änderung des Konsums zur Änderung des Einkommens heißt bekanntlich marginale Konsumquote:
Der Multiplikator
[The marginal propensity to consume] is of considerable importance, because it tells us how the next increment of output will have to be divided between consumption and investment. For ΔYw = ΔCw + ΔIw, where Cw and Iw are the increments of consumption and investment; so that we can write ΔYw = kΔIw, where 1 - 1/k is equal to the marginal propensity to consume.
Let us call k the investment multiplier. It tells us that, when there is an increment of aggregate investment, income will increase by an amount which is k times the increment of investment.
[2] c = ΔC/ΔY.
Eingesetzt in [1] folgt
[3] ΔY = cΔY + ΔI
[4] ΔY - cΔY = ΔI
[5] (1-c) ΔY = ΔI
![]() [7] ΔY
= kΔI
[7] ΔY
= kΔI
Dabei ist 1-1/k gleich der marginalen Konsumquote c. Keynes nennt k den Investitionsmultiplikator. Der Begriff Investitionsmultiplikator ist auch heute durchaus üblich, meist spricht man aber vom Multiplikator oder einfachen Einkommensmultiplikator. Gleichung [7] enthält eine bedeutsame Aussage:
Bei einem Multiplikator k steigt das gesamtwirtschaftliche Einkommen infolge eines Anstiegs der Investitionen um das k-fache des Anstiegs der Investitionen.
Da die marginale Konsumquote als bekannt angenommen werden kann, lässt sich der Wert des Multiplikators leicht berechnen:
![]() [8]
[8] ![]() .
.
Bei einer marginalen Konsumquote von 0,75 wäre der Multiplikator also 4. Oder etwas weniger technisch formuliert: Wenn die Investitionen um eine Milliarde EUR zunehmen, dann steigt die Produktion um vier Milliarden!
Das muss jeden Wirtschaftspolitiker elektrisieren, wenn er es zum ersten Mal hört - ... und versteht. Man muss "nur" einen Euro ausgeben, um das Einkommen um vier Euro ansteigen zu lassen. Mal unterstellt, dass Steuern diesen Prozess nicht stören, würde das bei einer Steuer auf das zusätzliche Einkommen (Grenzsteuer) in Höhe von 25 Prozent ja bedeuten, dass man ein höheres Einkommen "für lau" bekäme.
Wir wollen für unser Zahlenbeispiel überlegen, in welchem Umfang die Investitionen steigen, so dass das Vollbeschäftigungseinkommen YVB in Höhe von 1200 erreicht wird. Mit den Parameterwerten Caut = 100, Iaut = 100 und c = 0,75 hatten wir ein Gleichgewichtseinkommen in Höhe von
[9] ![]()
ermittelt. Es ist also eine Einkommenssteigerung ΔY von 400 erforderlich, um die Nachfragelücke zu schließen. Wenn wir die Werte in Gleichung [6] einsetzen
[10] ![]() ,
,
finden wir die notwendige Veränderung der Investitionen
[11] ΔI = 100.
Um zu begreifen was passiert, ist es äußerst hilfreich, sich einen zeitlichen Ablauf der Veränderungen vorzustellen. Dazu sei angenommen, die Unternehmen prognostizieren Änderungen der Nachfrage korrekt. Die Haushalte richten Ihren Konsum am Einkommen der Vorperiode aus. Dafür mag als Begründung z.B. herhalten, dass das Einkommen am Ende der Periode ausgezahlt wird. Alternativ könnte man auch davon ausgehen, dass nicht tagtägliche Anschaffungen geplant werden müssen, oder dass die Haushalte für die kommende Periode ein Einkommen in Höhe der aktuellen Periode erwarten ("statische Erwartungen").
Sie können die Ausführungen hier
nur verstehen, wenn Sie sich über
die ![]() Identität
von Produktion und
Identität
von Produktion und
Einkommen im Klaren sind!
Die beschriebene Konstellation heißt Robertson-Lag (Robertson-Verzögerung). Für unser dynamisches Modell der "bescheidensten Art" - so die nebenstehende Literaturempfehlung - gehen wir in Fortführung unseres Zahlenbeispiels von folgender Situation aus: In Periode 0 befindet sich die Wirtschaft seit längerem in der deflatorischen Lücke mit einem Einkommen in Höhe von 800. Der Staat, der bisher nicht in das Wirtschaftsgeschehen eingegriffen hat, sieht Handlungsbedarf und kündigt ein Beschäftigungsprogramm an. Ab der nächsten Periode (z.B. ein Monat) will er dauerhaft 100 investieren.
Die Unternehmen planen daraufhin, die Produktion in der kommenden Periode 1 von 800 auf 900 zu erhöhen. Da die Betriebe nicht ausgelastet sind, stellt die Realisierung kein Problem dar. Es werden die benötigten Arbeitskräfte eingestellt und Produktion und Einkommen steigen auf 900.
In der nächsten Periode kommt es zu einem sekundären - man könnte auch sagen: indirekten - Nachfrageffekt. Da das Einkommen in der Vorperiode 900 betrug, steigt die um eine Periode verzögert reagierende Konsumnachfrage an:
[12] ![]()
Die vorausschauenden Unternehmen planen daher für Periode 2 eine Produktion von
[13] ![]() .
.
Um die zusätzlichen Güter im Wert von 75 herzustellen, werden weitere Einstellungen vorgenommen. Die Einkommenssituation verbessert sich, woraufhin die Konsumnachfrage abermals steigt:
[14] ![]()
Die Unternehmen kommen der gestiegenen Nachfrage nach und produzieren in Periode 3
[15] ![]() .
.
Der Anstieg des Einkommens von Periode 2 auf Periode 3 fällt allerdings etwas geringer aus als in der Vorperiode. In Abbildung 1, die den Prozess noch für ein paar weitere Perioden zeigt, erkennt man den Grund. Jede Einkommenssteigerung führt anteilig im Ausmaß der marginalen Konsumquote zu einer Nachfragesteigerung. Der Primäreffekt des Staates hat die Produktion um 100 steigen lassen. Dieses vermehrte Einkommen in den Taschen der Haushalte induziert einen Anstieg der Konsumnachfrage von 75 (blaue Markierungspunkte in Abb. 1), da die marginale Konsumneigung 0,75 beträgt.
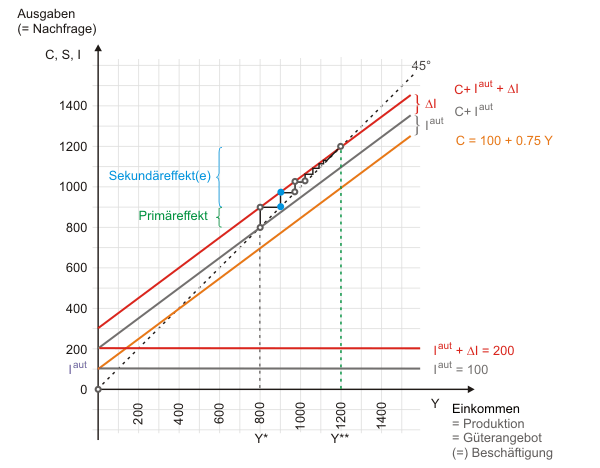
"Dynamisierter" Multiplikator (Robertson-Lag): Der Primäreffekt zieht eine Folge von Sekundäreffekten nach sich. Jeder Euro Einkommenssteigerung löst einen Anstieg der Nachfrage um den Betrag der marginalen Konsumquote in der Folgeperiode aus, die ihrerseits wieder zu einem Einkommensanstieg führt. Da die marginale Konsumquote kleiner als 1 ist, läuft sich der Prozess tot.
Die Unternehmen produzieren die zusätzlich nachgefragten Konsumgüter. Der Einkommensanstieg in Höhe von 75 löst abermals einen Anstieg der Konsumnachfrage aus, allerdings nur noch in Höhe von
[16] ![]() .
.
In der nächsten Periode wird sich der Anstieg der Konsumnachfrage weiter abschwächen:
[17] ![]() .
.
Und so läuft sich der Prozess langsam aber sicher tot.
Nach theoretisch unendlich vielen Perioden - in der Abbildung erkennen Sie aber, dass der Großteil des Anpassungsvorgangs sehr zügig abgeschlossen ist - werden die Konsumausgaben um
[18] ![]()
angestiegen sein.* Die gesamte Nachfrage steigt um
[19] ![[19]](../gifs/Multiplikator_G19.gif)
Die nachstehende Tabelle zeigt den Prozess bis Periode 25. In Periode 0 befindet sich der Markt im Gleichgewicht. Es gilt I=S. In Periode 1 entsteht durch den Start des Beschäftigungsprogramms eine Überschussnachfrage, die in ungeplantem Sparen von 100 resultiert.
Die gestiegenen Nachfragewünsche der Haushalte lassen die Manager in den Unternehmen frohlocken und die Produktion und damit das Einkommen ansteigen. Da die Haushalte aber 25 Prozent ihres jeweiligen Einkommensanstiegs sparen, hat der Kreislauf von Periode zu Periode Sickerverluste. Nach zehn Perioden ist die Überschussnachfrage kaum mehr der Rede wert.
|
Periode |
Y |
I |
ΔI |
C |
Sgepl |
Sungepl |
|
|
|
|
|
|
|
|
|
1 |
900,00 |
100,00 |
100,00 |
700,00 |
100,00 |
100,00 |
|
2 |
975,00 |
100,00 |
100,00 |
775,00 |
125,00 |
75,00 |
|
3 |
1.031,25 |
100,00 |
100,00 |
831,25 |
143,75 |
56,25 |
|
4 |
1.073,44 |
100,00 |
100,00 |
873,44 |
157,81 |
42,19 |
|
5 |
1.105,08 |
100,00 |
100,00 |
905,08 |
168,36 |
31,64 |
|
6 |
1.128,81 |
100,00 |
100,00 |
928,81 |
176,27 |
23,73 |
|
7 |
1.146,61 |
100,00 |
100,00 |
946,61 |
182,20 |
17,80 |
|
8 |
1.159,95 |
100,00 |
100,00 |
959,95 |
186,65 |
13,35 |
|
9 |
1.169,97 |
100,00 |
100,00 |
969,97 |
189,99 |
10,01 |
|
10 |
1.177,47 |
100,00 |
100,00 |
977,47 |
192,49 |
7,51 |
|
11 |
1.183,11 |
100,00 |
100,00 |
983,11 |
194,37 |
5,63 |
|
12 |
1.187,33 |
100,00 |
100,00 |
987,33 |
195,78 |
4,22 |
|
13 |
1.190,50 |
100,00 |
100,00 |
990,50 |
196,83 |
3,17 |
|
14 |
1.192,87 |
100,00 |
100,00 |
992,87 |
197,62 |
2,38 |
|
15 |
1.194,65 |
100,00 |
100,00 |
994,65 |
198,22 |
1,78 |
|
16 |
1.195,99 |
100,00 |
100,00 |
995,99 |
198,66 |
1,34 |
|
17 |
1.196,99 |
100,00 |
100,00 |
996,99 |
199,00 |
1,00 |
|
18 |
1.197,74 |
100,00 |
100,00 |
997,74 |
199,25 |
0,75 |
|
19 |
1.198,31 |
100,00 |
100,00 |
998,31 |
199,44 |
0,56 |
|
20 |
1.198,73 |
100,00 |
100,00 |
998,73 |
199,58 |
0,42 |
|
21 |
1.199,05 |
100,00 |
100,00 |
999,05 |
199,68 |
0,32 |
|
22 |
1.199,29 |
100,00 |
100,00 |
999,29 |
199,76 |
0,24 |
|
23 |
1.199,46 |
100,00 |
100,00 |
999,46 |
199,82 |
0,18 |
|
24 |
1.199,60 |
100,00 |
100,00 |
999,60 |
199,87 |
0,13 |
|
25 |
1.199,70 |
100,00 |
100,00 |
999,70 |
199,90 |
0,10 |
Beachten Sie bitte, dass ΔI nicht die Veränderung der Investitionen von Periode zu Periode anzeigt, sondern die Veränderung gegenüber dem Ausgangsniveau.
Ja. Der Staat hätte anstelle von Investitions- auch Konsumgüter nachfragen können. Ob die Ausgaben sinnvoll sind oder nicht, spielt keine Rolle. Im Extremfall beschäftigt der Staat Arbeitskräfte, die er im Winter die Autobahnen mit Schaufeln von Eis und Schnee und im Sommer mit Besen vom Staub befreien lässt. Das wäre zwar ineffizient, um nicht zu sagen idiotisch, aber in unserem Modell macht es keinen Unterschied. Ob in der Gleichung zur Bestimmung des Gleichgewichtseinkommen
[20] ![[20]](../gifs/Multiplikator_G20.gif)
der Wert von Caut oder von Iaut ansteigt - auf das Einkommen wirkt es sich kurzfristig gleichermaßen aus. Die mittel- bis langfristigen allokativen Wirkungen werden vom Modell nicht erfasst.
Der Staat muss auch nicht unbedingt selbst als Nachfrager
auftreten. Es würde bereits vollkommen genügen, wenn er durch die Verbreitung
von Optimismus die Unternehmen zu vermehrten Investitionen bewegen könnte.
Wenn der Wirtschaftsminister glaubhaft versichert, ab jetzt ginge es nur noch
bergauf, und die Unternehmen die Investitionen erhöhen, kommt der Multiplikatoreffekt
genau so in Gang, wie wir es eben gesehen haben. Ebenso könnte der Minister
die Konsumenten ermutigen, ihre Konsumausgaben zu erhöhen, so dass Caut steigt.
Wenn eine Ermutigung wegen des Vertrauensverlustes durch die bisherige Politik
nicht reichen sollte, ließe sich mit erhöhten Transferzahlungen nachhelfen
(s. ![]() Staatsausgabenmultiplikator).
Staatsausgabenmultiplikator).
Wichtig ist, dass die Bürger den Aufschwung erwarten. Wenn sie im Vertrauen auf den Aufschwung ihre Ausgaben erhöhen, erfüllen sich ihre Erwartungen von selbst. Diese Erkenntnis wird oft mit dem Wort umschrieben, die Wirtschaft bestünde zu fünfzig Prozent aus Psychologie. Sie liefert ein Argument, warum ein bloßer Wechsel der Regierung einen Aufschwung auslösen kann.
Umgekehrt kann natürlich auch ein negativer Multiplikatorprozess in Gang kommen, wenn sich Pessimismus breit macht und das Vertrauen in die Regierung schwindet. Verstärken die Haushalte z.B. wegen Zukunftsängsten ihre Sparanstrengungen, dann reduzieren die Unternehmen im Ausmaß des Nachfrageausfalls die Produktion, da sie nicht auf Lager produzieren werden. Dadurch sinken aber Beschäftigung und Einkommen, was den Konsum abermals zurückgehen lässt.
Welche Wirkung eine Nachfrageänderung letztlich entfaltet,
ist nach ![]() Gleichung [7] offensichtlich abhängig von der Höhe des Multiplikators:
Gleichung [7] offensichtlich abhängig von der Höhe des Multiplikators:
![]() [21]
[21] ![]()
Da für die marginale Konsum- und Sparneigung nur Werte zwischen 0 und 1 sinnvoll sind, liegt der Wert des Multiplikators auf jeden Fall über 1. Und zwar um so mehr, je größer die marginale Konsumneigung bzw. je kleiner die marginale Sparquote ist.
Zur Verdeutlichung betrachten wir den extremen Fall einer marginalen Sparquote in Höhe von 1. Das gesamte zusätzliche Einkommen, das den Haushalten zufließt, wird gespart.
Wenn der Staat in dieser Situation seine Ausgaben erhöht, indem er z.B. in den Straßenbau investiert, dann entsteht durch diesen Primäreffekt unmittelbar Beschäftigung. Der Sekundäreffekt bleibt allerdings aus, da aus dem zusätzlichen Einkommen keine Konsumnachfrage entsteht. Das ist sehr unrealistisch, aber es sollte ja auch nur die folgende Aussage illustrieren, die erklärt, warum der Wirtschaftsminister bei schwacher Konjunktur die Bürger kaum anhalten wird, mehr zu sparen.
Der Multiplikator ist um so kleiner, je höher die marginale Sparquote ist.
Graphisch lässt sich der Zusammenhang zwischen Multiplikator und marginaler Sparneigung in Abbildung 2 erkennen.
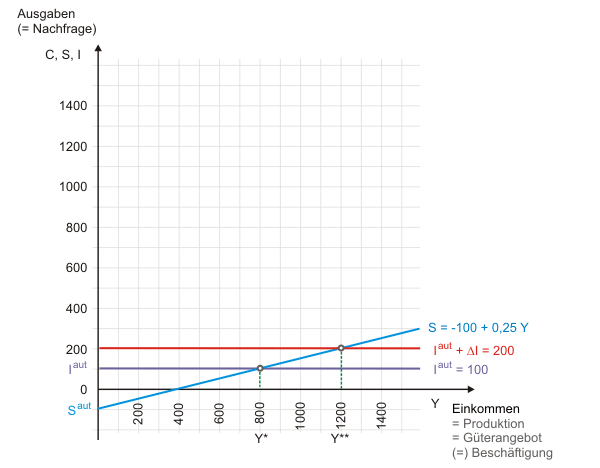
[Maussensitive Grafik] Der Multiplikator ist um so größer, je geringer die marginale Sparquote ist.
Bei einer marginalen Sparquote von 0,25 lässt eine dauerhafte Anhebung der Investitionen um 100 das Gleichgewichtseinkommen von Y* um 400 auf Y** steigen. Das maussensitive Diagramm zeigt Ihnen zum Vergleich den Multiplikatoreffekt einer marginale Sparquote von 0,167.
Damit sich die Multiplikatorwirkung auf Dauer entfaltet, muss die auslösende Nachfragesteigerung selbst von Dauer sein. Wenn sie das nicht ist, der Staat also z.B. ein einmaliges Konjunkturprogramm auflegt und seine Ausgaben anschließend wieder auf das vorherige Maß zurückfährt, spricht man von einem Nachfrageimpuls.
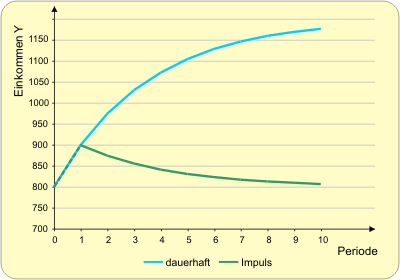
Nachfrageimpuls: Die einkommenssteigernde Wirkung einer
einmaligen
Nachfrageerhöhung ist nicht von Dauer. Die blaue Kurve
zeigt zum
Vergleich den Anpassungspfad bei einer dauerhaften Nachfragesteigerung.
Ein solcher Impuls kann (in unserem Modellrahmen) nicht von
dauerhafter Wirkung sein, da sich das Gleichgewichtseinkommen ![]() Gleichung
[20] zufolge nach Abschluss der Anpassungsprozesse wieder auf seinen
ursprünglichen
Wert einstellen muss. Abbildung 3 zeigt, wie sich im Robertson-Lag-Zahlenbeispiel
ein einmaliger Nachfrageimpuls in Höhe von 100 im Zeitablauf auswirkt.
Gleichung
[20] zufolge nach Abschluss der Anpassungsprozesse wieder auf seinen
ursprünglichen
Wert einstellen muss. Abbildung 3 zeigt, wie sich im Robertson-Lag-Zahlenbeispiel
ein einmaliger Nachfrageimpuls in Höhe von 100 im Zeitablauf auswirkt.
In der ersten Periode dehnen die Unternehmen die Produktion um den Betrag der gestiegenen Nachfrage aus. In der zweiten Periode fällt die Nachfrage aber nicht sofort auf ihr ursprüngliches Niveau zurück, da das um im Vergleich zur Ausgangssituation um 100 höhere Einkommen in Periode 1 die Konsumnachfrage in Periode 2 um 75 steigen lässt. Die Einkommenssteigerung klingt also um so schneller ab, je geringer die marginale Konsumquote ausfällt.
Mit der nachstehenden interaktiven Tabelle können Sie die Zahlenbeispiele dieses Abschnitts - beliebige andere natürlich ebenso - nachrechnen. Anstelle von ΔI wird in der Simulation das Symbol G für Staatsausgaben benutzt, da nicht nur Veränderungen der Ausgaben um einen fixen Betrag simuliert werden, sondern beliebige Veränderungen der Ausgaben in jeder Periode vorgenommen werden können.
Um den in Abbildung 3 dargestellten Impuls zu simulieren, tragen Sie in Periode 1 für G den Wert 100 ein. Um die dauerhafte Erhöhung der Investitionen vorzunehmen, schalten Sie das Kontrollkästchen unter der Tabelle ein.